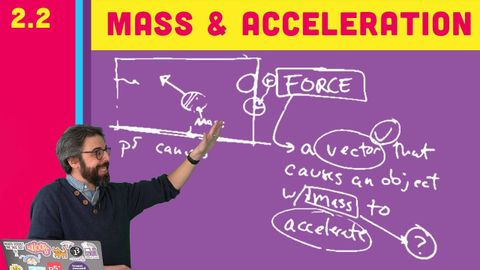
Placeholder Image

字幕列表影片播放

    字幕與單字

    00
    收藏
    影片單字

    ultimately

    US /ˈʌltəmɪtli/

    ・

    UK /ˈʌltɪmətli/

    • adv.最終，最後；根本地；極其
    B1 中級多益高級英檢
    更多
    demonstrate

    US /ˈdɛmənˌstret/

    ・

    UK /'demənstreɪt/

    • v.t./i.顯示；表露；遊行；演示；證實； 展示
    A2 初級多益中級英檢
    更多
    scale

    US /skel/

    ・

    UK /skeɪl/

    • n. (c./u.)大小；規模；魚鱗；比例；等級；標尺
    • v.t./i.測量；攀登；魚鱗
    A2 初級多益初級英檢
    更多
    arbitrary

    US /ˈɑrbɪˌtrɛri/

    ・

    UK /ˈɑ:bitrəri/

    • adj.任意的；獨斷的；任意的；武斷的；不講理的；專斷的
    B1 中級多益高級英檢
    更多
    使用能量
    解鎖所有單字
    解鎖發音、解釋及篩選功能
    energy point vocabulary