Subtitles & vocabulary
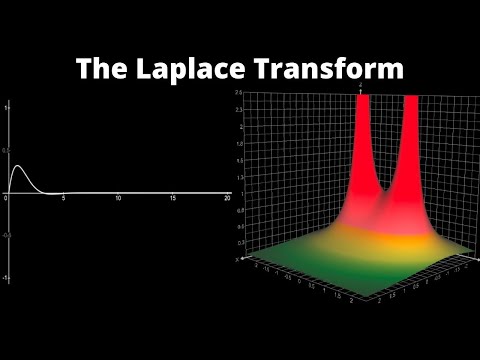
What does the Laplace Transform really tell us? A visual explanation (plus applications)
00
Sujuku posted on 2022/11/16Save
Video vocabulary
entire
US /ɛnˈtaɪr/
・
UK /ɪn'taɪə(r)/
- Adjective
- Complete or full; with no part left out; whole
- Undivided; not shared or distributed.
A2TOEIC
More essentially
US /ɪˈsenʃəli/
・
UK /ɪˈsenʃəli/
- Adverb
- Basically; (said when stating the basic facts)
- Used to emphasize the basic truth or fact of a situation.
A2
More assume
US /əˈsum/
・
UK /ə'sju:m/
- Transitive Verb
- To act in a false manner to mislead others
- To believe, based on the evidence; suppose
A2TOEIC
More eventually
US /ɪˈvɛntʃuəli/
・
UK /ɪˈventʃuəli/
- Adverb
- After a long time; after many attempts; in the end
- At some later time; in the future
A2
More Use Energy
Unlock Vocabulary
Unlock pronunciation, explanations, and filters
