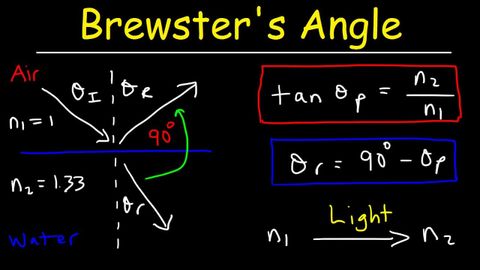
布儒斯特角、光的偏振、偏振角 - 物理問題 (Brewster's Angle, Polarization of Light, Polarizing Angle - Physics Problems)
kevin 發佈於 2024 年 10 月 02 日  沒有此條件下的單字
沒有此條件下的單字US /spɪˈsɪfɪk/
・
UK /spəˈsɪfɪk/
US /ɪˈkwɪvələnt/
・
UK /ɪˈkwɪvələnt/
US /əˈprəʊtʃ/
・
UK /ə'prəʊtʃ/
- v.t./i.逼近;找...商量
- n. (c./u.)通道;入口;接洽;處理方式;方法
US /məˈtɪriəl/
・
UK /məˈtɪəriəl/
- n. (c./u.)布料;素材;資料;材料;物質
- adj.重要的;物質的