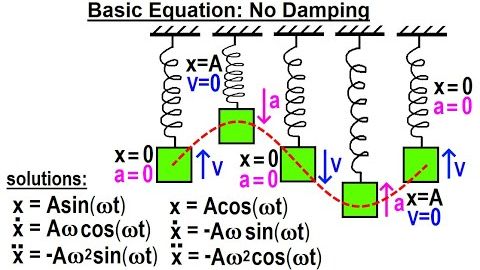
物理學:第 16.1 章 有阻尼的簡諧運動(20 箇中的 1 個) 基本方程:無阻尼 (Physics: Ch 16.1 Simple Harmonic Motion with Damping (1 of 20) Basic Equation: No Damping)
 沒有此條件下的單字
沒有此條件下的單字US /ɪˈsenʃəli/
・
UK /ɪˈsenʃəli/
- adv.本質上 ; 本來 ; 實質上;本質上;實際上
- v.t.裝出;假裝;以為;(想當然地)認為;承擔;就任
US /ˈkɑnstənt/
・
UK /'kɒnstənt/
US /ˈriəˌlaɪz/
・
UK /'ri:əlaɪz/