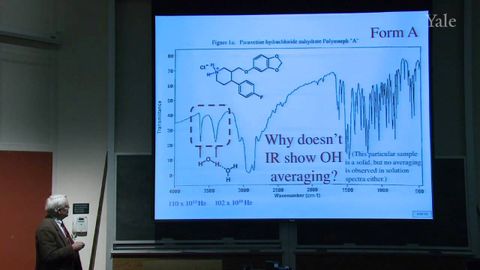
25.C-13和2D NMR。親電性芳烴取代 (25. C-13 and 2D NMR. Electrophilic Aromatic Substitution)
Cheng-Hong Liu 發佈於 2021 年 01 月 14 日  沒有此條件下的單字
沒有此條件下的單字US /ˈævərɪdʒ, ˈævrɪdʒ/
・
UK /'ævərɪdʒ/
- n. (c./u.)平均
- v.t.算出...的平均數
- adj.平均的;一般的,通常的;中等的
- v.t.連結;拴在一起;發生性關係;配對
- n. (c./u.)配偶;一對;一些相同或相似的人、事、物;幾個
- n.(知識)領域;專業;田野;場地;球場;戰場;欄位;場
- v.t.巧妙地回答;接(球);派…上場;接球
- adj.野外的
- v.t./i.變化,改變;轉移,移動;輪班
- n. (c./u.)轉移;輪班職工;班;輪班;輪班;連衣裙;地殼變動;換檔鍵;換檔
- adj.輪班的